- Adjusted Rand index
Clustering 평가 방법인 Adjusted Rand index에 대해 알아보겠습니다. ARI의 경우 타깃값을 아는 경우에 쓰이는 방법인 것을 다시한번 말씀드립니다.
저번에 포스팅한 Rand index에 대해 보고 오시는걸 추천 드립니다.
또한, wikipedia에 자세한 설명이 나와 있습니다.
- Adjusted Rand index 수식
contingency table이 있을 때

ARI는 다음과 같이 계산할 수 있습니다.

Adjusted Rand index 수식은 크게 보면 총 4가지로 나타낼 수 있습니다.
아래 예시를 통해 이해해보겠습니다.
- Adjusted Rand index 예시
앞서 Rand index에서 사용한 예시를 가져와 수식을 알아보겠습니다.
저와 친구 4명이 있었습니다. [태구, 영수, 영희, 철수, 동우] 저희는 새학기를 맞아 새로운 반을 배정받았는데
1반 : 태구, 2반 : 영수, 영희, 3반 :철수 동우로 배정받았습니다. [1, 2, 2, 3, 3]
사실 저와 친구들은 반 배정 전 누가 같은반이 될까 내기를 한적이 있습니다. 그 중 제가 예상한 결과는
1반 : 태구, 영수 2반 : 영희, 철수, 동우였습니다. [1, 1, 2, 2, 2]
그렇다면 반배치 결과(타깃값)와 저의 예상을 ARI로 계산해보겠습니다.
우선 contingency table을 만들어 보겠습니다. X와 Y는 클러스터 입니다.
X - 태구 예측 클러스터 = [1, 1, 2, 2, 2]
Y = 반배정(타깃값) = [1, 2, 2, 3, 3]
우선 contingency table을 만들겠습니다.
| X / Y | Y1 | Y2 | Y3 | sums |
| X1 | 1 | 1 | 0 | 2 |
| X2 | 0 | 1 | 2 | 3 |
| sums | 1 | 2 | 2 |
Y1,Y2,Y3에 비해 X1,X2만 있는 이유는 태구 예측 클러스터에 군집이 1과2밖에 없기 때문입니다.
X클러스터에서 태구를 1반으로 예측하였고 Y클러스터의 태구또한 1반 이므로 X1 / Y1 = 1입니다.
또한, 영수를 1반으로 예측하였지만, Y클러스터의 영수는 2반이기 때문에 X1 / Y2 = 1입니다.
예를들어 Y클러스의 영수 또한 1반으로 배정되었다면 X1 / Y1 = 2 입니다.
이제 contingency table을 직접 만들 수 있겠죠?
그럼 이제 ARI 값을 구해 보겠습니다.
nij의 경우는 각표에 할당된 값이며, ai의 경우 행의 합 bj의 경우 열의 합입니다. 표를 통해 해당값을 구하게 되면 아래와 같습니다.

최종적인 ARI값 :
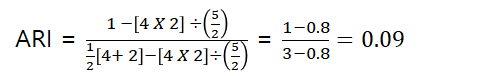
- Python을 이용한 ARI 계산

파이썬 사이킷런 라이브러리를 이용하면 쉽게 ARI결과를 예측할 수 있습니다.
위의 계산과 같은 값이 나왔네요!
- ARI에 대한 생각
기존에 같은 예시를 통해 Rand index값을 구했을 경우는 0.6으로 높은값이 나왔지만 ARI는 0.09로 나왔습니다.
ARI가 0일 경우 무작위할당과 같은 수치이며, 0.2이하의 점수는 좋지않은 성능을 나타낸나고 합니다.
Rand index는 예측 군집수가 많아질 수록 클러스터 내에 군집되지 않는 pair가 많아지면서 성능이 높아지는 단점이 있었습니다. 그러나 Adjusted Rand index의 경우 위의 예시와 같이 모든 경우(클러스터 수 )에 대해 고려되기 때문에 점수에 대한 신뢰성이 높아진다고 생각합니다.
'통계' 카테고리의 다른 글
| Rand index란? (2) | 2020.05.08 |
|---|---|
| 통계개념 (0) | 2019.11.18 |
| 통계에서 사용되는 bootstrap의 의미는 무엇인가요 (0) | 2019.11.15 |
| ROC curve? (0) | 2019.11.09 |
| 혼돈행렬(confusion matrix)에 대해 알아보자 (2) | 2019.11.07 |