Taegu

이전다음

0123

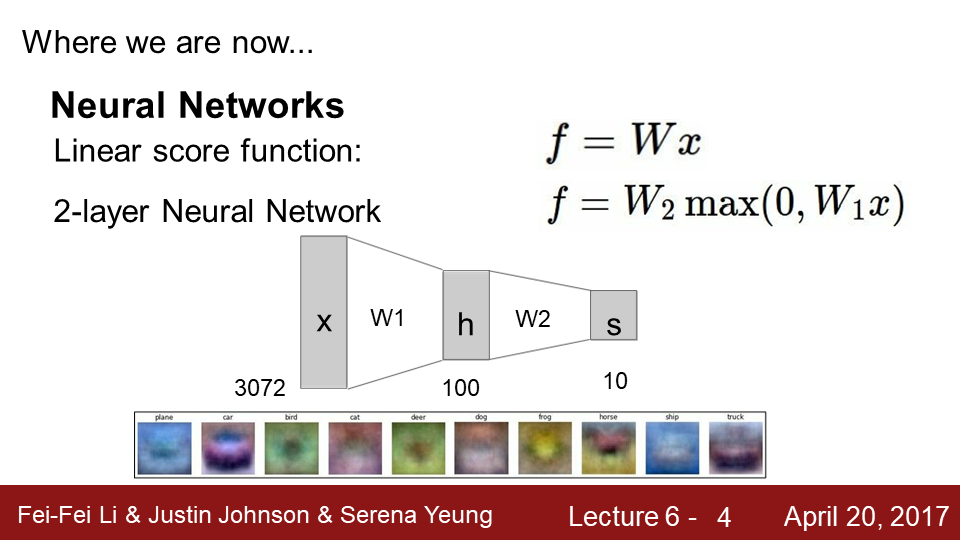
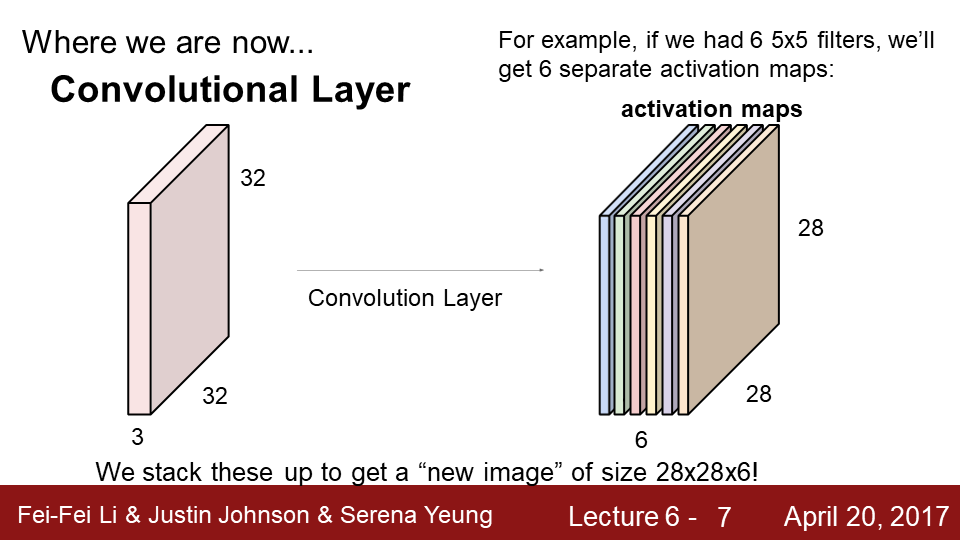
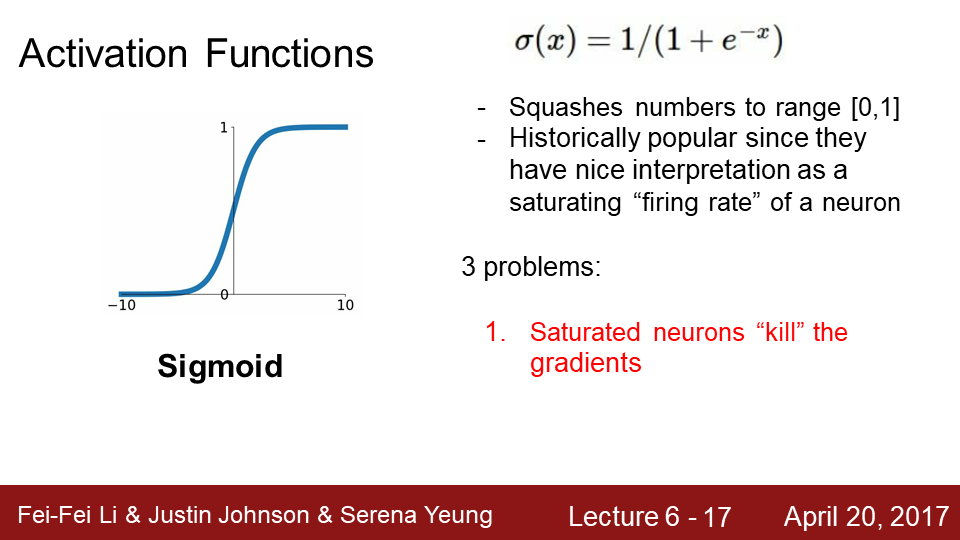
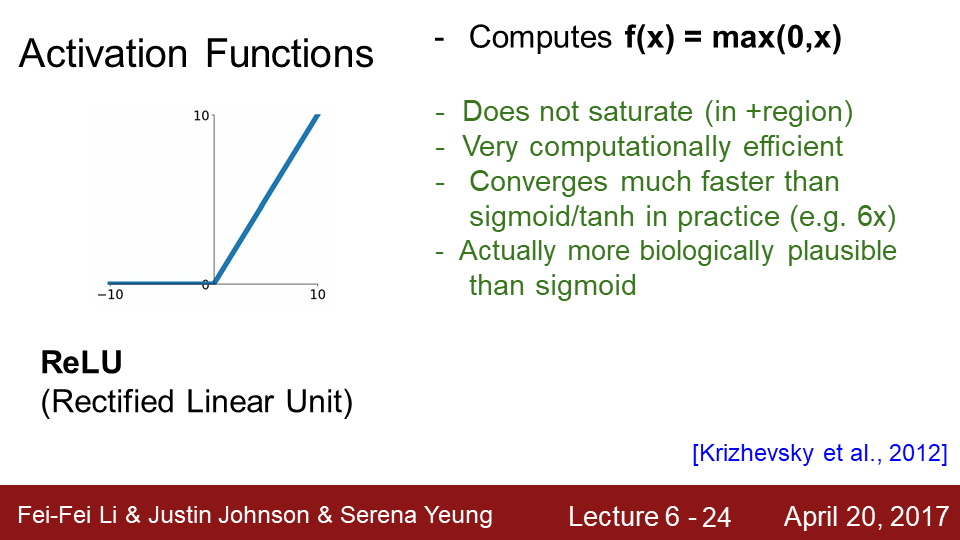
9-1 오늘은 CNN 구조에 대해 알아보겠습니다.
9-2 AlexNet, VGG, GoogLeNet, ResNet에 대해 알아보고 다른 CNN 구조에 대해서도 알아보겠습니다.
9-3 Lenet-5은 산업에 성공적으로 적용된 최초의 conv모델입니다.  숫자인식에서 크게성공하여 우체국 산업에서 적용되었습니다.
9-4 Subsampling에서 Average pooling을 썻으며 non overlapping polling이 적용되었습니다. non overlapping polling이란 필터의 크기와 stride의 크기가 같아 중복되지 않고 polling하는 기법입니다. 자세한건 LeNet-5구현을 참조하시기 

바랍니다.

이전다음

012345678910111213

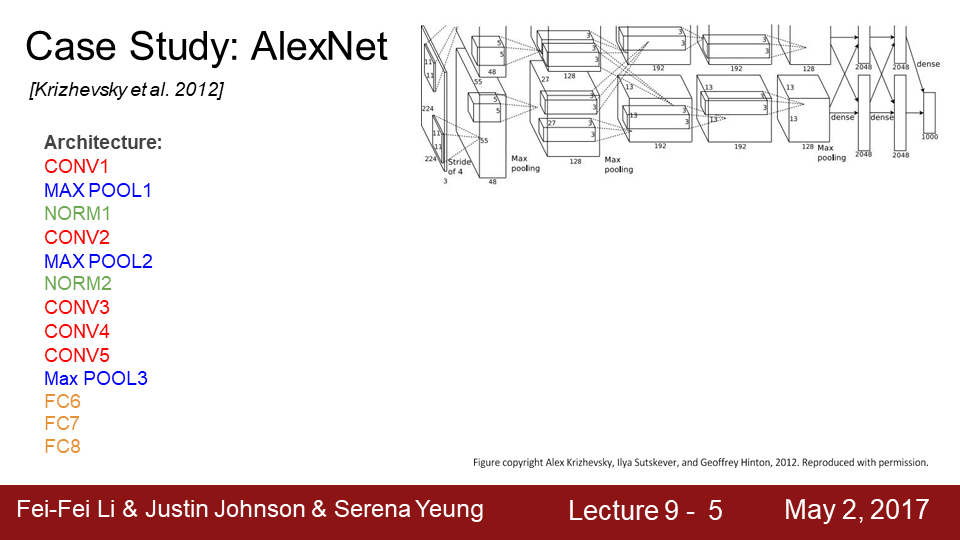
9-5 이번에는 AlexNet에 대하여 알아보겠습니다. AlexNet 12년에 등장해서 딥러닝을 부흥시켰습니다. 그이유는 

최초로 ImageNet대회에서 CNN으로 우승했기 때문입니다. 구조는 LeNet-5와 비슷하고 레이어만 증가했습니다.
9-6 227x227x3 이미지에 11x11사이즈에 stride가4인 96개의 필터를 적용하면 output volume 사이즈는 어떻게 될까요? 먼저 높이와 너비의 계산 공식은 (전체 이미지 크기- 필터크기 + 2*padding size) / stride+1입니다. 
9-7 정답은 55x55x96(필터갯수) 입니다. 그렇다면 이 Layer의 파라미터 수는 몇개일까요? 
9-8 파라미터의 갯수는 공식은 필터사이즈 x 입력depth x 필터갯수 입니다. 그렇다면 (11*11*3)*95 = 35,000개가 됩니다.
9-9 그렇다면 두번째 레이어를 살펴볼까요? 두번째는 풀링 레이어 입니다. Alexnet에서는 maxpooling을 사용합니다 output volume 사이즈는 어떨까요?
9-10 앞의 공식을 적용하면 27x27x96이 됩니다 그렇다면 파라미터의 갯수는 몇개일까요?
9-11 0개입니다. 당연하겠죠? pooling layer는 단순 downsampling로 파라미터가 없습니다.
9-12 이렇게 conv와 pooling가 반복되어 AlexNet을 구성합니다
9-13 AlexNet의 전체구조입니다. 그림에 input 사이즈가 224라고 나와있지만 실제로는 227입니다. 총 5개의 conv와 

3개의 max pool 2개의 FC로 구성됩니다.
9-14 AlexNet을 디테일하게 살펴보면 ReLU를 처음 사용하였습니다. 그리고 Norm으로 local response normalization사용하였는데 현재는 사용하지 않습니다. 많은 augmentation을 사용하였으며 0.5의 dropout을 사용했습니다. 학습률을 0.01에서 검증 auc가 평평해지면 10으로 나누어 추가적인 학습을 진행했습니다. 그외는 표에 나와있는 것과 같습니다.
9-15 AlexNex이 개발되었을 시대에는 컴퓨팅파워가 낮아 3GB의 GPU밖에 없어 AlexNet으로 ImageNet을 학습시킬 수 없었습니다. 그래서 model parallel을 통해 두개의 GPU을 연결해 병렬로 처리했습니다. 그래서 자세히 그림을 

보시며 conv1에서 depth가 96이아니라 48입니다.
9-16 CONV1, CONV2, CONV4, CONV5의 경우 같은 GPU끼리 feature maps을 연결하고있으며
9-17 CONV3, FC6, FC7, FC8의 경우는 2개의 GPU가 모든 feature maps을 연결하고있습니다.

이전다음

012345678910111213

9-19 앞서 본 AlexNet은 12년도 ImageNet에서 우승했습니다. 그 뒤에 이어서 ZFNet이 13년도 ImageNet우승을 

차지했습니다. 
9-20 ZFNet 은 AlexNet과 유사하지만 11x11 with stride4의 필터를 7x7 with stride 2로 바꾸었으며 기존의 

CONV3, 4, 5의 필터갯수를 384, 384, 256에서 512, 1024, 512로 바꾸었습니다.
9-21 다음은 14년도 ImageNet 우승작을보겠습니다. 먼저 ImageNet 2등과 localization대회에서 2등을 차지한 VGGNet의 구조를 알아보겠습니다. localization대회란 기본적으로 "이미지에 고양이가 있는지?" 를 분류하는 것 뿐만 아니라 정확히 고양이가 어디에 있는지 네모박스를 그리는 것입니다.
9-22 VGGNet의 특징은 더 깊어지고 더 작은 필터를 사용했다는것입니다. 이웃픽셀을 포함할 수 있는 가장작은 필터인 3x3 필터를 사용했습니다. 그리고 작은 필터를 유지하고 주기적으로 pooling을 수해했습니다.
9-23 왜 작은 필터를 사용할까요? 우선 필터의 크기가 작으면 파라미터의 수가 적고 depth를 더 키울 수 있습니다.
9-24 3x3 with stride1 CONV를 3번 쌓게 되면 effective receptive field는 무엇일까요? 
9-25 정답은 7x7입니다. 왜 이렇게 되는지 살펴보겠습니다.
보충 첫 번째 layer에서 하나의 픽셀은 CONV를 통해 3x3의 정보를 가지게 됩니다 두 번째 레이어에서 하나의 픽셀은 3x3의 정보를 가진 상태에서 또다시 3x3의 CONV를 통해 5x5의 정보를 가집니다. 이런식으로 3x3의 CONV를 3번 쌓게되면 7x7의 effective receptive field 가지게 됩니다.
9-26 effective receptive field을 이해했다면 왜 이렇게 할까요? 그 이유는 좀 더 깊은층을 쌓을 수 있으며 비선형함수를 더 쌓기때문에 표현이 자유로워 집니다. 또, 파라미터의 갯수가 줄어듭니다.

앞서 파라미터의 갯수는 필터의크기 x 입력의 depth x 필터의 갯수라고 했죠? 그렇다면 3x3xCxC가 세번 쌓이기 때문에 3*(3*3*C*C) = 27*C*C가 됩니다. 7x7의 파라미터 갯수는 어떻게 될까요? 7*7*C*C = 49*C*C로 두배가까이 차이가 납니다. 왜 입력의 depth와 필터의 갯수가 같아야하나? 왜 같은C인가? 의문이 있다면 같은 입력과 출력을 가져야만 effective receptive field를 가질 수 있기때문입니다. 이부분은 다른 포스팅을 통해 한번 더 다루겠습니다.
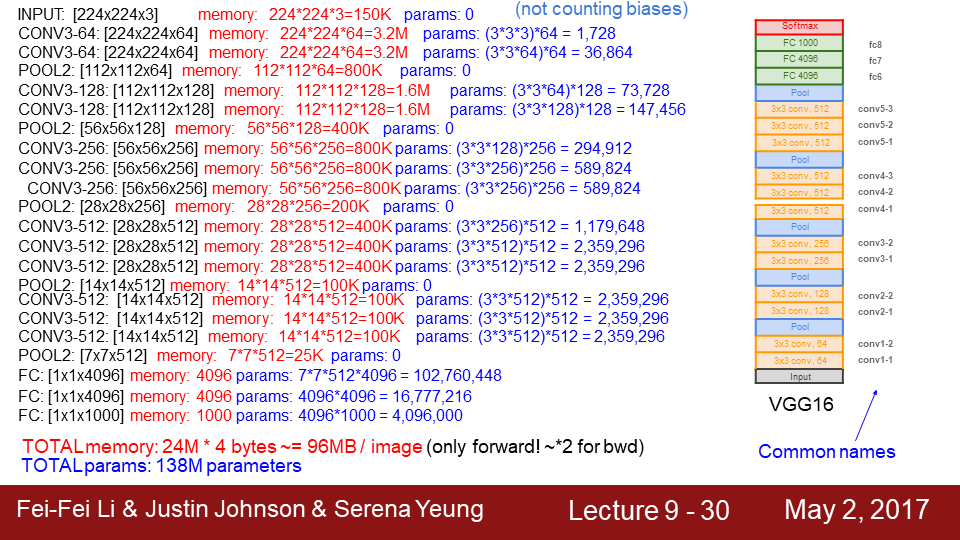
9-27 VGGNet의 전체 구조입니다.
9-28 Total memory는 한번의 forward pass시 필요한 메모리를 계산한것입니다. 각노드가 4bites의 메모리를 차지하기 때문에 약 100mb입니다. 전체 메모리가 5gb라면 이미지 하나당 100mb이므로 50장밖에 처리할 수 없습니다. 

그리고 전체 파라미터의 개수는 1억3800만개 이며 AlexNet경우에는 6000만개 였습니다.
9-29 앞부분에서 메모리가 많이 들며 FC에서 파라미터 개수가 많습니다 그래서 최근에는 FC를 없애는 추세입니다.
9-30 CONV를 지칭하는 방법이며 기억하시면 논문을 읽는데 도움이 될 것 같습니다.
9-31 VGG의 마지막 FC-layer FC7은 아주 좋은 feature representation 특징 추출이 잘되며 다른 task에도 일반화가 뛰어납니다. 학습절차는 AlexNet과 비슷하며 LRN은 사용하지 않았고 최종결과 중 BEST를 앙상블 했습니다.

이전다음

01234567891011121314

9-32 이제 14년도  ImageNet우승 모델인 GooGleNet을 살펴보겠습니다.
9-33 GooGleNet은 효율적인 계산력을 가진 깊은 모델입니다. 총 22개의 layer을 가지고 효율적은 Inception이라는 모듈을 가집니다. FC layer은 없으며(많은 파라미터 때문), AlexNet보다 12배 적은 500만개의 파라미터를 가집니다.
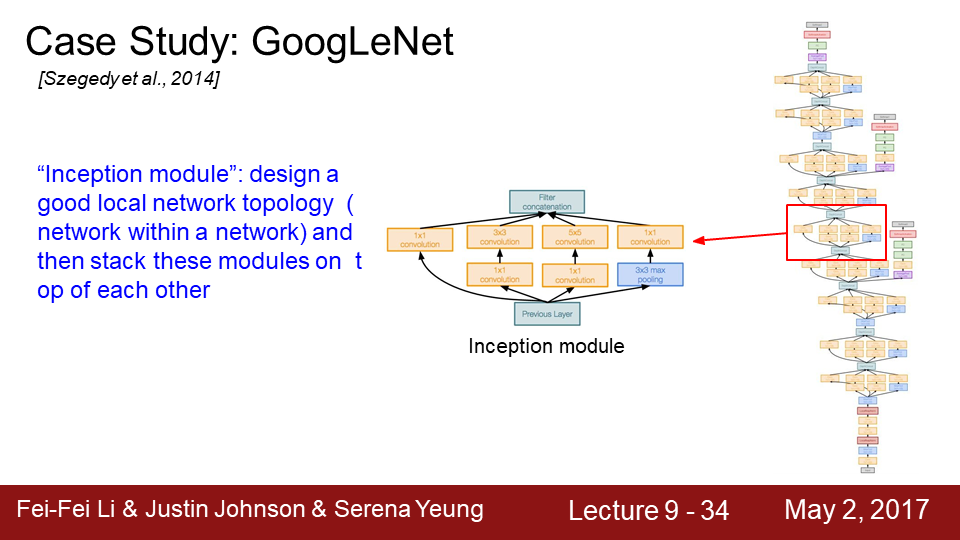
9-34 인셉션 모듈은 network 안에 network 즉 good local network topology를 만들다는 생각에서 출발했습니다. 
9-35 Local network 를 인셉션 모듈이라 하는데 인셉션 모듈 내에는 동일한 입력은 받는 서로다른 다양한 필터들이

병렬로 존재합니다. 1x1 / 3x3 / 5x5 CONV에 Pooling도 있습니다. 여기에서는3x3 pooling이죠 각 레이어에서 각각의

출력 값들이 나오는데 그 출력들을 모두 Depth 방향으로 합칩니다(concatenate). 그렇게 합치면 하나의 tensor로 출력이 결정되고 이 하나의 출력을 다음 레이어로 전달하는 것입니다.
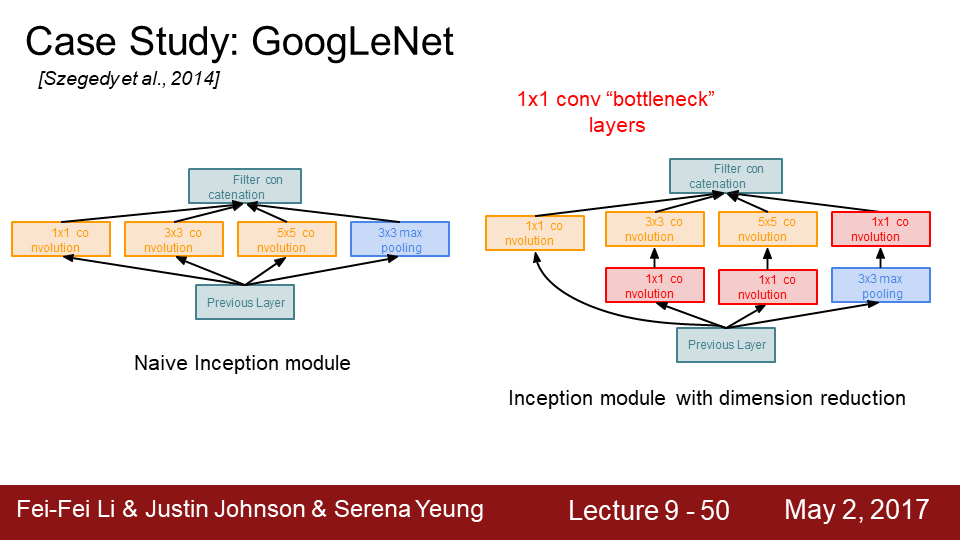
9-36 지금까지는 다양한 연산을 수행하고 이를 하나로 합쳐준다는아주 단순한 방식(naive way)을 살펴봤습니다. 그렇다면 이 network의 문제점은 뭘까요?
9-37 문제는 바로 계산 비용에 있습니다. 
9-38 1x1 conv with 128 filters의 output 사이즈는 몇일까요?
9-39 28x28x128입니다.
9-40 다른 filter의 output 사이즈는 어떻게될까요?
9-41 input 사이즈의 크기에서 필터의 갯수에 따라 output사이즈를 가집니다. 
9-42 모든 필터를 합쳤을 때 output사이즈는 어떨까요?
9-43 depth 기준으로 합친다고 했으니 28x28x672입니다. 
9-44 이 레이어들의 계산량을 한번 살펴봅시다 첫 번째 예시로 1 x 1 conv를 살펴봅시다. 1 x 1 conv는각 픽셀마다

1 x 1 x 256 개의 내적연산을 수행합니다. 따라서 픽셀 당 256번의 곱셈 연산이 수행되는 것이죠(Conv Ops:맨 뒤의 256) 그리고 픽셀이 총 28 x 28 이므로처음 "28  x 28" 이 여기에 해당합니다. 그리고 이런 연산을 수행하는 필터가 총 128개 있으므로 1 x 1 conv에서의 전체 연산량은28 x 28 x 128 x 256 입니다.  똑같이 나머지 레이어를 계산하면 8억5천4백만 flops가 됩니다. 매우 큽니다.
9-45 또한 pooling layer 또한 문제가 되는데 풀pooling layer 입력은 depth를 그대로 가져오기때문에 무조건 입력의 depth보다 커질 수 밖에 없습니다.
9-46 이 엄청난 계산량을 해결해주기 위해 bottleneck layer가 나왔습니다. bottleneck layer는 feature의 depth를 

줄여주는데 자세히 살펴보겠습니다.

이전다음

0123456789101112

9-47 1x1 conv를 다시 한번 살펴봅시다. 
9-48 1x1 conv는 각spatial location에서만 내적을 수행합니다. 그러면서 depth만 줄일 수 있습니다. 입력의 depth를더 낮은 차원으로 projection 하는 것입니다. Input feature map들 간의선형결합(linear combination) 이라고 할 수 있습니다. 주요 아이디어는 바로 입력의 depth를 줄이는 것입니다.
9-49 왼쪽 그림은 초기의 인셉션 모듈이고 오른쪽은 인셉션 모듈에 bottleneck layer 적용한 모습입니다.
9-50 3x3, 5x5 CONV 전에 bottleneck layer가 추가되었고 3X3 POOL 뒤에 bottleneck layer가 추가되었습니다.
9-51 자 그럼 필터들의 output사이즈와 계산량을 구해보겠습니다. 결론을 말씀드리면 초기의 인셉션 모듈보다 두배  이상 계산량이 절감되었음을 볼 수 있습니다.
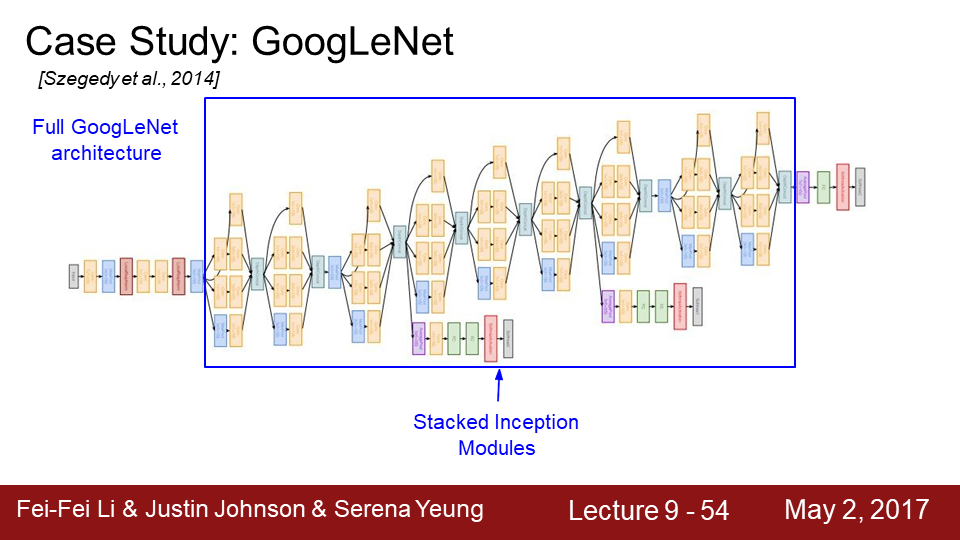
9-52 이러한 인셉션 모듈을 쌓아 만든 모델이 GoogLeNet입니다.
9-53 전체 GoogLeNet을 알아보겠습니다. 시작은 기존의 models과 비슷하게 CONV- POOL 구조를 가집니다.
9-54 그다음 중간에 인셉션 모듈을 쌓습니다.
9-55 마지막에 Classifier output이 있습니다.
9-56 GoogLeNet에서는 계산량이 많은 FC-layer를 대부분 걷어냈고 파라미터가 줄어들어도 모델이 잘 동작함을 

확인했습니다.
9-57 그리고 여기 보시면 추가적인 줄기가 뻗어있는데이들은 보조분류기(auxiliary classifier) 입니다.이것들은 단지 작은 미니 네트워크들입니다. Average pooling과 1x1 conv가 있고 FC-layer도 몇개 붙습니다.

그리고 SoftMax로 1000개의 ImageNet class를 구분합니다. 그리고 실제로 이 곳에서도ImageNet trainset loss를

계산합니다. 네트워크의 끝에서 뿐만 아니라 이 두 곳에서도 Loss를계산하는 이유는 네트워크가 깊기 때문입니다.

보조분류기를 중간 레이어에 달아주면 추가적인 그레디언트를 얻을 수 있고, 따라서 중간 레이어의 학습을 도울 수 있습니다.
9-58 전체 아키텍쳐의 모습입니다.가중치를 가진 레이어는 총 22개입니다. 각 Inception Modul 은 1x1/3x3/5x5 conv layer를병렬적으로 가지고있습니다.
9-59 지금까지 14년도 ImageNet 우승 모델인 GoogLeNet을 살펴봤습니다.

이전다음

0123456

9-60 다음은 15년도 ImageNet모델인 ResNet을 살펴보겠습니다. 깊이의 혁명이라 불릴 정도로 ResNet모델의 depth는 기존의 모델보다 매우 깊습니다.
9-61 ResNet은 residual connections을 사용한 매우 깊은 모델입니다. 이제 ResNet에 대해 알아보겠습니다.
9-62 만약에 CONV를 깊게 쌓는다면 어떨까요? 예를들어 VGGNet의 CONV를 엄청 늘리면 성능이 어떻게될까요? 
9-63 그림은 20레이어와/56의 레이어의 모델 성능을 나타냅니다. 오른쪽의 test error의 경우는 56레이어가 20레이어보다 안좋습니다. 더 깊은 네트워크가 안좋을 수 있구나 생각할 수 있습니다. 
9-64 그러나 training error를 보면 조금 이상합니다. 깊은 네트워크가 있다면 당연히 엄청나게 많은 파라미터로 인해 

오버피팅 되겠구나 예상할텐데 training error또한 20레이어보다 안좋고 이는 오버피팅 때문이 아니였습니다. 
9-65 Resnet저자들의 가설은 모델학습시 최적화에 문제가 있다고 생각하고 모델이 깊어질수록 최적화가 어렵다고 

생각했습니다. 
9-66 그들은 "모델이 더 깊다면 적어도 더 얕은 모델만큼은성능이 나와야 하지 않은지"라고 추론했습니다. 가령 이런 

해결책을 생각해 볼 수 있습니다. 우선 더 얕은 모델의가중치를 깊은 모델의 일부 레이어에 복사합니다. 그리고 나머지 

레이어는 identity mapping을 하는 것이죠(input을 output으로 그냥 내보냄) 이렇게 구성하면 shallower layer 만큼의 

성능을 나와야겠죠 Deeper Model의 학습이 제대로 안되더라도적어도 Shallow Model 만큼의 성능은 보장됩니다. 

그렇다면 이 motivation을 우리가 만들 모델에 녹이려면어떻게 모델 아키첵쳐를 디자인해야할까요?

이전다음

0123456789101112

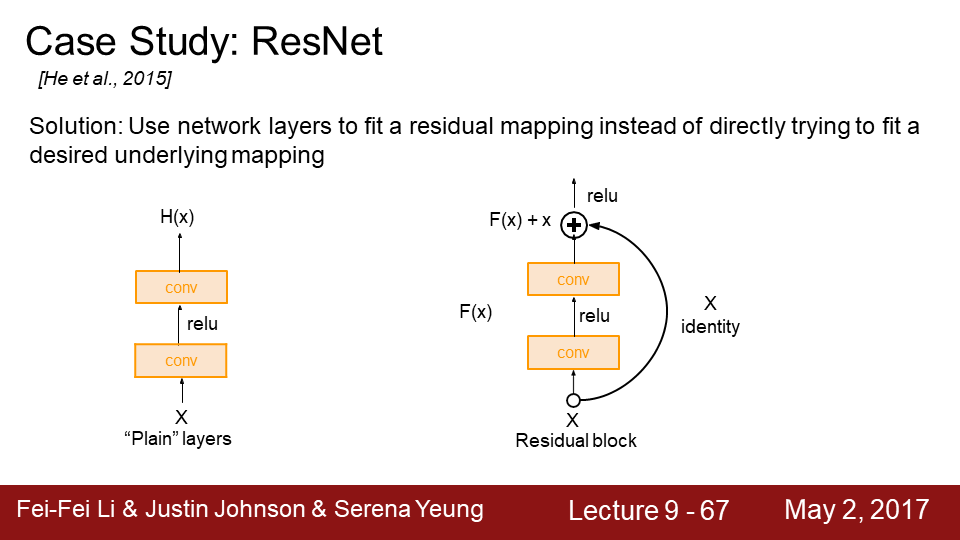
9-67 그들의 아이디어는 레이어를 단순하게 쌓지 않는 것입니다. 
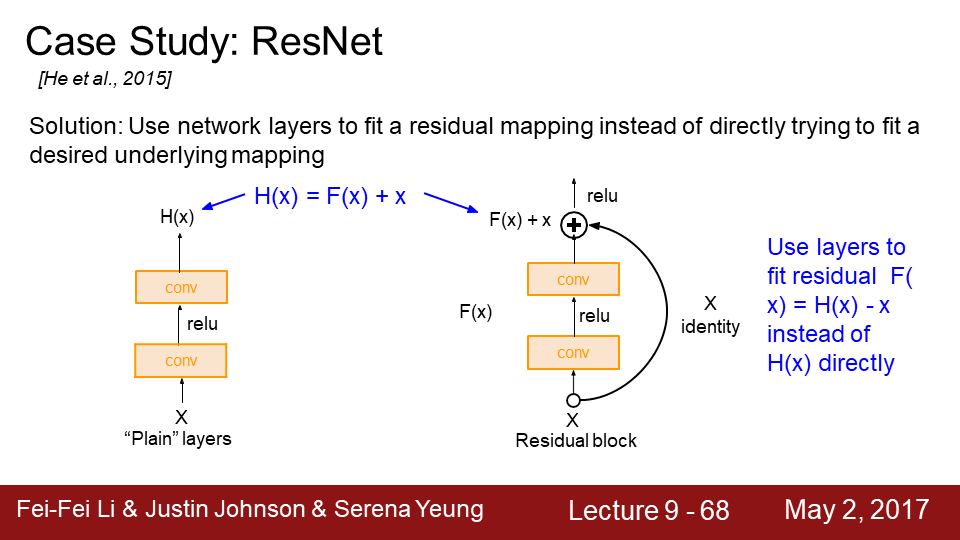
9-68 레이어가 직접 "H(x)"를 학습하기 보다이런 식으로 "H(x) - x" 를 학습할 수 있도록 만들어줍니다. 이를 위해서 

Skip Connection을 도입하게 됩니다.오른쪽의 고리모양 보이시죠 오른쪽의 Skip Connection은 가중치가 없으며 입력을 identity mapping으로 그대로 출력단으로 내보냅니다. 그러면 실제 레이어는 변화량(delta) 만 학습하면 됩니다. 

입력 X에 대한 잔차(residual) 이라고 할 수 있죠Direct mapping 대신 Residual mapping을 하도록이런 식으로 블럭을 

쌓는 것이죠 최종 출력 값은 "input X + 변화량(Residual)" 입니다. 이 방법을 사용하면 학습이 더 쉬워집니다.

가령 Input = output 이어야 하는 상황이라면 레이어의 출력인 F(x)가 0 이어야 하므로(residual = 0) 모든 가중치를 

0으로 만들어주면 그만입니다. 결론적으로 H(x)의 값을 훈련시키기 어려우니 x+f(x)를 통해 x의 변화량을 측정하는 것이 

더 효율적이다라는 이야기입니다. 그렇다면 이 아이디어가 아까 위에 나온 아디디어 처럼 Shallow Model 만큼의 성능은 보장될 수 있습니다. 만약 그전 Shallow Model layer의 가중치를 업로드하고 그전보다 성능이 안좋다면 나머지 layer에 가중치가 0이 되어 Shallow Model의 성능은 나온다는 이야기입니다.
9-69 여기 전체 ResNet 아키텍쳐를 보실 수 있습니다. 하나의 Residual blocks는 두 개의 3x3 conv layers로이루어져 

있습니다. 이렇게 구성해야 잘 동작하는 것으로 알려져있습니다.
9-70 그리고 주기적으로 필터를 두배 씩 늘리고stride 2를 이용하여 Downsampling을 수행합니다.
9-71 시작은 CONV layer로 시작합니다.
9-72 그리고 네트워크의 초반에는 Conv Layer가 추가적으로 붙고네트워크의 끝에는 FC-Layer가 없습니다. 대신

Global Average Pooling Layer 를 사용합니다.GAP는 하나의 Map 전체를 Average Pooling 합니다.
9-73 전체 depth에 따라 34, 50, 101, 152모델이 있습니다.
9-74 ResNet의 경우 모델 Depth가50 이상일 때 Bottleneck Layers를 도입합니다. 이는 GoogLeNet에서 사용한 방법과 유사합니다. Bottleneck Layer는 1x1 conv를 도입하여초기 필터의 depth를 줄여줍니다. 
9-75 가령 입력이 28x28x256 일때 1x1 conv를 적용하면 depth가줄어들어서 28x28x64 가 됩니다. 이로인해 

3 x 3 conv의 계산량이 줄어듭니다. 그리고 뒤에 다시 1x1 conv를 추가해서 Depth를 다시 256으로 늘립니다.

Deeper ResNet은 이런 구조를 취합니다.
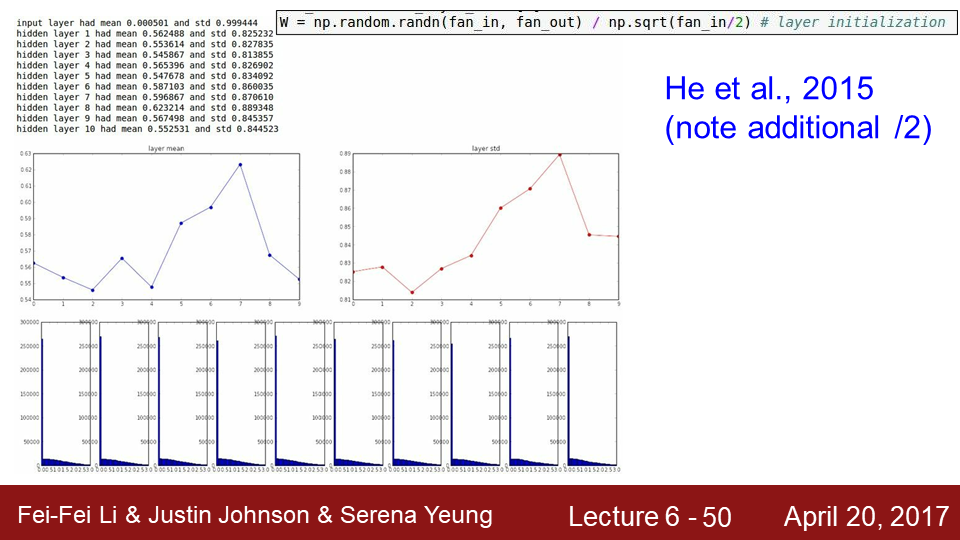
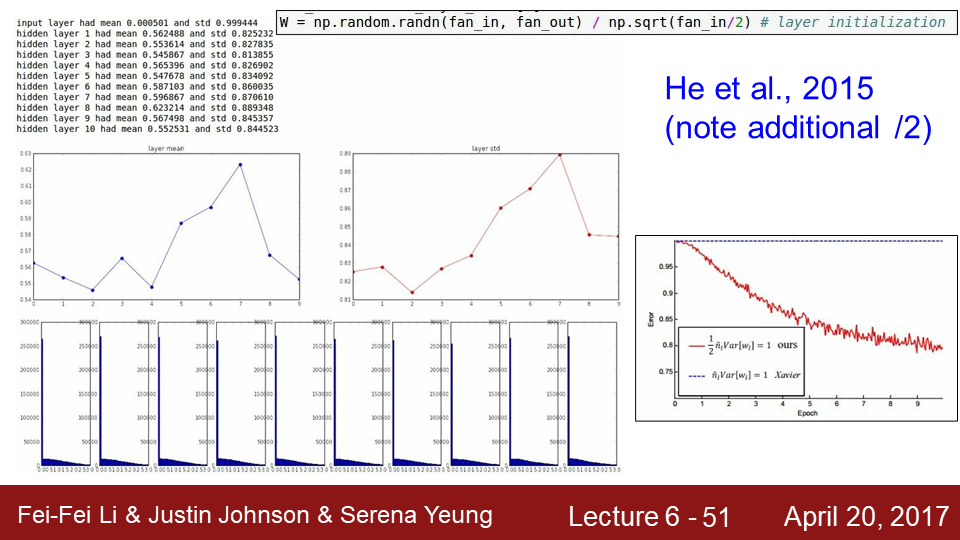
9-76 ResNet의 training 방법은 우선 CONV 이후 Batch Normalization을 사용했으며 Xavier/2 인 가중치를 사용했으며 나머지는 그림과 같이 적용했습니다.
9-77 ResNet은 다른모델과 압도적인 차이를 벌리며 모든 대회에서 우승했습니다.
9-78 그리고 최초로 ImageNet에서 인간을 이긴 모델이됩니다.
9-79 이시점에서 ImageNet대회는 마감하게됩니다.

이전다음

0123456

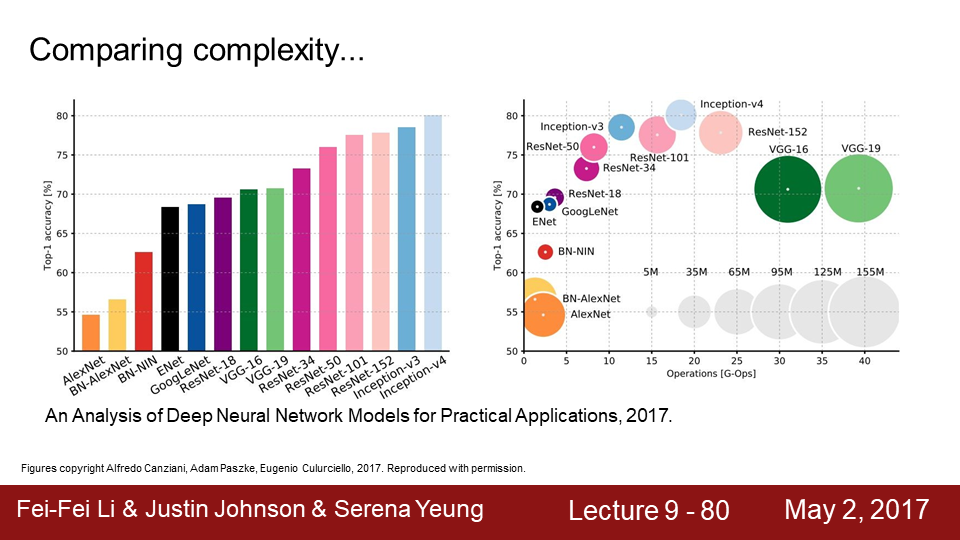
9-80 자 그럼 모델 별 complexity를 빠르게 한번 살펴보겠습니다.  왼쪽 그래프는 모델의 성능 별로 정렬해 보았습니다 .Top-1 Accuracy가 기준이고 높을수록 좋은 모델입니다. 자 이제는 오른쪽 그래프를 살펴봅시다. 연산량과 메모리가 추가되었습니다. Y축은 top-1 Accuracy이고 높을수록 좋습니다. X축은 연산량을 나타냅니다. 오른쪽으로 갈수록 연산량이 많습니다.원의 크기는 메모리 사용량입니다. 원이 클수록 덩치가 큰 모델이죠.
9-81 거의 모두 우리가 지금까지 배운 모델이거나 조금 변형된모델들 입니다. 가령 GoogLe-inception을 보시면이 

모델은 버전별로 V2, V3 등이 있는데 가장 좋은 모델은 바로 여기V4 입니다. ResNet + Inception 모델입니다.
9-82 VGGNet의 경우는 메모리도 크고 연산량도 많이 최근에는 사용하지 않습니다.
9-83 GoogLeNet이 가장 효율적인 네트워크입니다. x축에서거의 왼쪽에 있죠 뿐만 아니라 메모리 사용도 적습니다.
9-84 AlexNet의 경우 연산량은 적으나 메모리도 크고 정확도 또한 낮습니다 VGG와 마찬가지로 사용하지 않습니다.
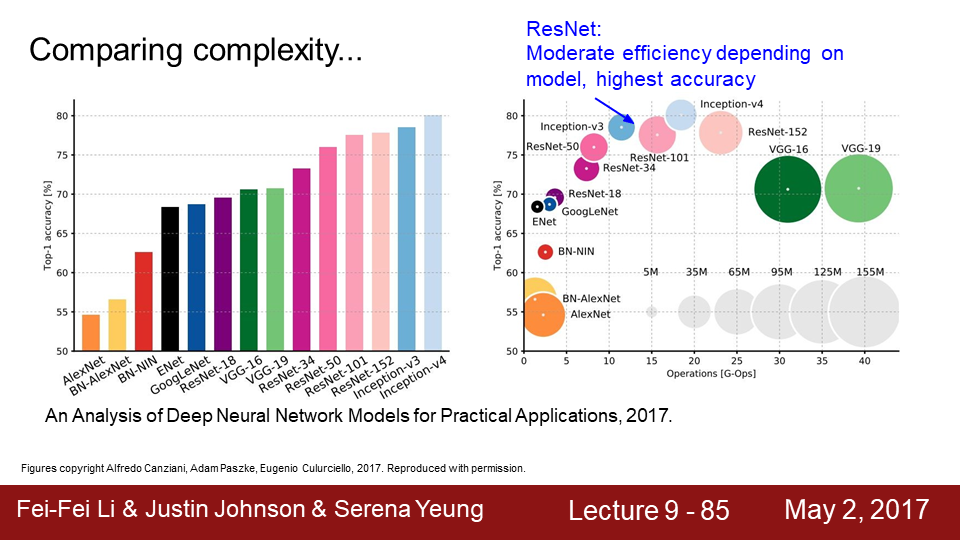
9-85 ResNet으 적당한 연산량과 메모리를 가지며 높은 정확도를 나타내 최근에도 사용되며 많이 개발되고 있는 모델입니다.
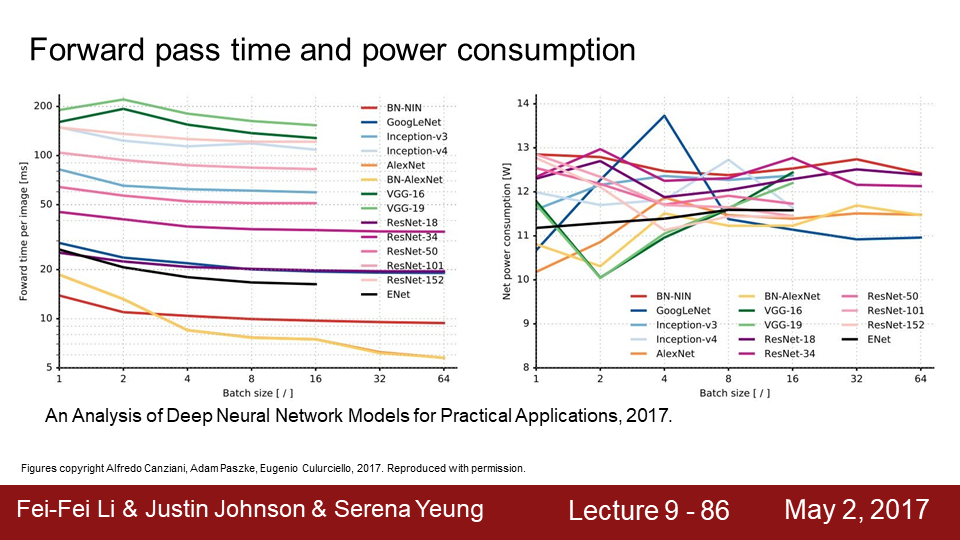
9-86 왼쪽 그래프는 forward pass 시간입니다. 단위는 ms 인데VGG가 제일 오래걸립니다. 200ms으로 초당 5정도 처리할 수 있겠군요

이전다음

012345678910

9-87 이제 다른 CNN모델 구조에 대해 보겠습니다.
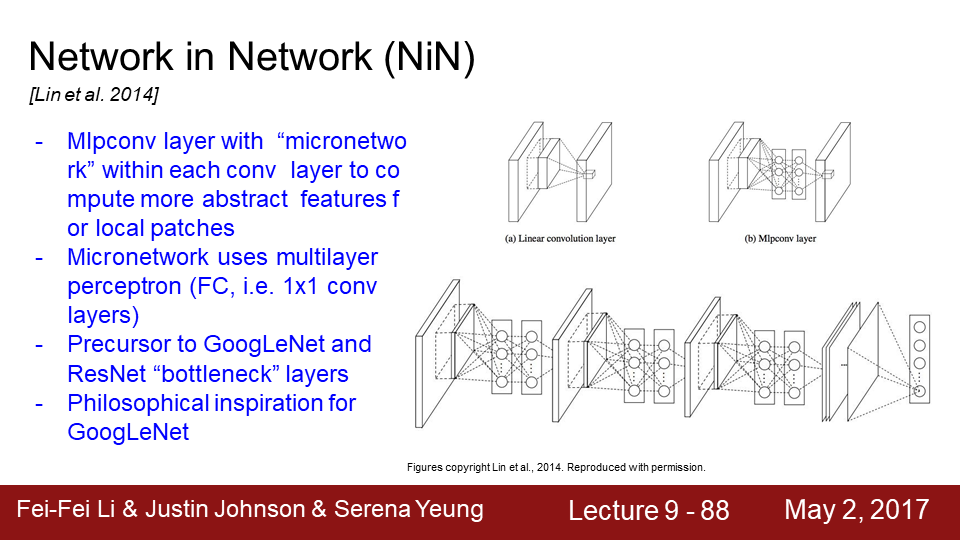
9-88 Network in Network 입니다.2014년에 나온 논문입니다. Network in Network의 기본 아이디어는 네트워크 안에 작은 네트워크를 삽입하는 것이죠 각 Conv layer 안에 MLP(Multi-Layer Perceptron)를 쌓습니다. FC-Layer 몇 개를 쌓는 것이죠맨 처음에는 기존의 Conv Layer가 있고 FC-Layer를 통해 abstract features를 잘 뽑을수 있도록 합니다 단순히 conv filter만 사용하지 말고, 조금 더 복잡한 계층을만들어서 activation map을 얻어보자는 아이디어입니다. NIN에서는 기본적으로는 FC-Layer를 사용합니다. 이를 1x1 conv layer 라고도 합니다. Network in Network는 GoogLeNet과 ResNet보다 먼저 Bottleneck 개념을 정립했기 때문에 아주 의미있는 아이디어입니다. 또한 GoogLeNet은 NIN와 구조는 조금 다르지만 NIN의 "철학적인 영감" 을 받았습니다.
9-89 2016년 ResNet의 저자들은 ResNet의 블록 디자인을 향상시킨 논문을 발표했습니다. 이 논문에서는 ResNet block path를 조절하였습니다. 새로운 구조는 direct path를 늘려서 정보들이 앞으로 더욱 더 잘 전달되고 Backprob도 더 잘 될 수 있게 개선했습니다. 이 새로운 Block 구조 덕분에 더 좋은 성능을 얻을 수 있었습니다.
9-90 Wide Residual Networks입니다. 기존의 ResNet 논문은 깊게 쌓는 것에 열중했지만 사실 중요한 것은 depth가 아닌 residual 이라고 주장했습니다. Residual Connection이 있다면 네트워크가 굳이 더 깊어질 필요가 없다고 주장했습니다. 그래서 그들은 residual block 을 더 넓게 만들었습니다. 즉 conv layer의 필터를 더 많이 추가했습니다. 가령 기존의 ResNet에는 Block 당 F개의 filter만 있었다면 대신에 F * K 개의 필터로 구성했습니다. 각 레이어를 넓게 구성했더니 50 레이어만 있어도 152 레이어의 기존 ResNet보다 성능이 좋다는 것을 입증했습니다. 그리고 네트워크의 Depth 대신에 filter의 갯수를 늘리면 추가적인 이점이 있는데, 계산 효율이 증가합니다. 왜냐하면 병렬화가 더 잘되기 때문입니다. 네트워크의 Depth를 늘리는 것은 sequential한 증가이기 때문에 conv의 필터를 늘리는(width) 편이 더 효율적입니다.
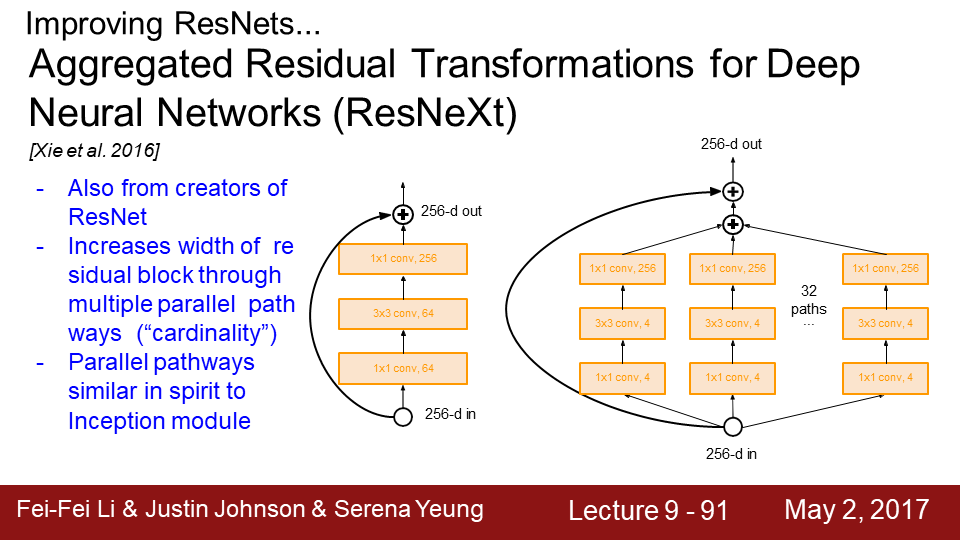
9-91 그리고 비슷한 시점에 등장한 또 하나의 논문이 있습니다. 바로 ResNeXt 입니다. 이 논문 또 ResNet의 저자의 논문입니다.계속해서 ResNet 구조를 밀고 있습니다. 여기에서도 계속 residual block의 width를 파고듭니다. filter의 수를 늘리는 것이죠 각 Residual block 내에 "다중 병렬 경로" 추가합니다. 이들은 pathways의 총 합을 cardinality라고 불렀습니다. 하나의 bottleneck ResNet block은 비교적 작지만 이런 얇은 blocks을 병렬로 여러개 묶었습니다. 또한 여러 Layers를 병렬로 묶어준다는 점에서Inception Module과도 연관있습니다.
9-92  Stochastic Depth 이라는 논문이 있습니다. 주제는 Depth 이죠 네트워크가 깊어지면 깊어질수록 Vanishing gradient 문제가 발생합니다. 깊은 네트워크에서는 그레디언트를 뒤로 전달할수록점점 그레디언트가 작아지는 문제가 있습니다. 기본 아이디어는 Train time에 레이어의 일부를 제거합니다.short network면 트레이닝이 더 잘 될 수 있기 때문입니다.일부 네트워크를 골라서 identity connection으로 만들어버립니다. 이렇게 shorter network를 만들어서 Train하면그레디언트가 더 잘 전달될 수 있겠죠 아주 효율적인 방법이 될 수 있습니다. Dropout과 유사합니다. 그리고 Test time에서는 full deep network를 사용합니다.
9-93 지금까지 소개시켜 드린 방법들은 ResNet 아키텍쳐를 개선하고자 노력했습니다. "Beyond ResNet"을 지향하는 방법들도 있습니다. Non-ResNets 중에도 ResNet과 견줄만한 성능의 모델들이 있습니다. 그 중 하나는 FractalNet 입니다. 아주 최근에 나왔습니다.그들은 residual connection이 쓸모없다고 주장합니다. FractalNet 아키텍쳐에서는 residual connection이 전혀 없습니다. 그들은 shallow/deep network의 정보 모두를 잘 전달하는 것이 중요하다고 생각했습니다. FractalNet에서는 shllow/deep 경로를 출력에 모두 연결합니다. FractalNet에는 다양한 경로가 존재하지만 Train time에는Dropout처럼 일부 경로만을 이용해서 Train 합니다. 그리고 Test time에는 full network를 사용합니다. 그들은 FractalNet의 좋은 성능을  입증했습니다.
9-94 DenseNet에는 Dense Block 이란 것이 있습니다. 여기 보시면 한 레이어가 그 레이어 하위의모든 레이어와 연결되어 있습니다.  Network의 입력이미지가 모든 Layer의 입력으로 들어갑니다. 그리고 모든 레이어의 출력이 각 레이어의 출력과 Concat 됩니다. 그리고 이 값이 각 Conv layer의 입력으로 들어갑니다. 이 과정에서 dimention을 줄여주는 과정이 포함됩니다.이들은 Dense Connection이 Vanishing gradient 문제를 완화시킬 수 있다고 주장합니다. 그리고 Dense connection은 Feature를 더 잘 전달하고더 잘 사용할 수 있게 해줍니다. 각 레이어의 출력이 다른 레이어에서도여러번 사용될 수 있기 때문입니다.
9-95  "squeeze layer"는 1x1 필터들로 구성되고, 이 출력 값이 1x1/3x3 필터들로 구성되는 "expand layer"의 입력이 됩니다. SqueezeNet는 ImageNet에서 AlexNet 만큼의Accuracy를 보이지만 파라미터는 50배 더 적었습니다. 그리고 SqueezeNet을 더 압축하면 AlexNet보다500배 더 작아지게 됩니다. SqueezeNet의 용량은 0.5Mb 밖에 안됩니다
9-96,97 지금까지 CNN의 구조에 대해 알아봤습니다. 현재 Efficientnet 시리즈 등 많은 모델이 나왔으니 논문을 읽어보시면 도움이 될 것 같습니다.

오늘은 Neural Networks을 학습시키는 방법에 대해서 공부하겠습니다.

이전다음

0123456

6-1 먼저 지난시간에 배운것을 복습하겠습니다.

6-4 뉴럴 네트워크에 대해서 자세히 배웠습니다. linear layer들이 있고 중간에 activation function으로 비선형함수를 적용하여 깊은 층을 쌓을 수 있었습니다. 선형함수를 쌓게 되면 예를들어 y(x)=h(h(h(x))) = c^3이 되어 마치 1개의 layer처럼 됩니다. 층을 쌓는게 의미가 없어지는 것이죠

6-5 cnn에 대해 자세히 배웠습니다. Cnn은 공간구조를 사용하기 위해 convolutional layer를 사용하는 형태입니다

6-6 

6-7 convolutional layer는 대개 다수의 필터를 사용했습니다. 그리고 각 필터는 서로 다른 activation map을 생성합니다. 지난번에 언급된것처럼 왼쪽의 깊이와 오른쪽의 깊이는 다르다는 점을 기억해야합니다. 왼쪽의 깊이 3은 이미지의 채널 즉 rgb를 의미하며 오른쪽의 6은 5x5x3의 크기인 6개의 필터가 스트라이드를 통해 얻어진 액티베이션 맵이고 각 액티베이션 맵은 입력의 공간적인 정보를 보존하고 있습니다.

6-8 optimization을 통해서 네트워크의 파라미터를 학습할수 있었습니다. Loss가 줄어드는 방향으로 학습하게 됩니다. 그리고 이는 gradient의 반대 방향으로 이동하는 것과 같습니다.

6-9 Mini-batch SGD는 1. 데이터에서 샘플을 뽑은 뒤 2. Forwar prop을 통해 loss를 얻습니다. 3. Backprop을 통해 gradients를 얻고 4. gradient를 통해 parameters를 업데이트합니다.

이전다음

012345678910111213

6-10 다음은 뉴럴네트워크를 학습시키는 방법에대해 알아보겠습니다.

6-11 우선 네트워크 초기설정에 관해 배우고 학습과정을 세팅하며 파라미터 업데이트 및 하이퍼파라미터 최적화를 배우겠습니다. 모델 앙상블 또한 배워보겠습니다.

6-12 part1에서는 Activation Functions, Data Preprocessing, Weight Initialization, Batch Normalization, Babysitting the Learning Process, Hyperparameter Optimization에 대해 배우겠습니다.

6-13 Activation Functions

6-14 Activation Functions은 들어오는 입력(앞의 함수의 출력값)에 총합을 출력신호로 변환하는 함수이다. 활성함수라고 말하며 뉴럴 네트워크의 활성함수는 모두 비선형함수를 사용합니다.

6-15 앞서배운 익숙한 Sigmoid함수도 보이고 생소한 함수들도 보입니다. 뒤에서 Activation Functions에 대해 자세히 알아보겠습니다.

6-16 먼저 Sigmoid함수입니다. 시그모이드함수는 들어오는 입력값에 대해 0~1사이의 값으로 출력하며 역사적으로 뉴런의 발화점을 saturate한다는 점에서 뉴런과 비슷한 역할을 한다고 생각했습니다.

6-17 그러나 시그모이드는 saturated되는 부분에서 gradients가 죽는다는 문제가 있습니다.

6-18 X가 -10일 경우 시그모이드는 flat(=saturated)되고 gradient는 0이 됩니다. 그리고 이값이 밑으로 내려가며 0에가 까운 값이 backprop되고 이부분에서 gradient가 죽게 되고 밑으로 0이 내려갑니다. 10의 경우도 마찬가지입니다. 0일경우에는 선형으로 잘 작동됩니다.

6-19 시그모이드의 두 번째 문제는 출력값이 0을 중심으로 되어있지않고 0~1의 양수값만 출력하는 것 입니다.

6-20 이게 왜 문제가 되냐면 시그모이드의 출력은 바로 뒤에 층의 입력값으로 들어가게됩니다.  그런데 모든 입력값이 양수로 들어가면 backporp시 weight의 gradients(DL/Dw)는 DL/Da * x(local graient)가 되고 DL/Da의 부호에 따라 모두 양수 또는 음수로 가중치가 업데이트 되게 됩니다. 여기서 x 는 sigmoid의 입력값이라고 가정합니다.

6-21 그 결과 파란색 선이 최적의 w vector이지만 빨간색 선과 같이 양수 또는 음수로 업데이트 되는 지그재그의 모양을 띄며 이는 매우 비효율적인 업데이트입니다.

6-22 세 번째 문제는 exp()를 통한 연산으로 계산 비용이 비싸다는 내용이지만 무시할 정도의 수준이라고 합니다.

6-23 tanh activation function은 -1~1사이의 출력값을 가집니다 zero centered로 앞의 sigmoid의 단점을 극복했습니다. 그러나 아직까지도 saturated된 부분에서 gradients가 죽는 문제가 있습니다.

이전다음

012345678910

6-24 activation function은 ReLU입니다. 최근 거의 ReLU만 쓴다고 말할 정도옵니다. ReLU의 장점은 양수방향으로 saturate되지 않는다는 점입니다. 그리고 max함수 사용으로 계산측면에서 효율이며 sigmoid나 tanh보다 6배 빠르게 수렴합니다. 다음 그림을 보면 tanh은 36epoch동안 0.25error에 다다른 반면 ReLU 는 6epoch만에 도달합니다.

6-25 ReLU 단점을 알아보면 zero-centered 하지 않습니다. 그리고 x<0 일 경우 어떨까요?

6-26 x가 -10일 경우 saturate됩니다. gradient가 0이 되겠죠, 그렇다면 x가 10일때는 어떻게 될까요? 선형 영역(linear regime)에 속합니다. x가 0일 때는 어떨까요? 0입니다.

6-27 기본적으로 ReLU는 gradient의 절반을 죽여버리는 셈입니다. 모델이 학습하는 동안 일부 뉴런이 0만을 출력하여 활성화 되지 않는 문제인데, 이러한 문제를 dead ReLU라고 합니다. Dead relu가 발생하는 주요 원인에는 2가지가 있는데 첫 번째 초기화를 잘 못한 경우 입니다. 초기화를 잘못하여 음수영역에 들어가면 ReLU의 경우 회복하지 못하고 죽어버립니다. 두 번째 학습률(Leraning rate)이 지나치게 높은 경우입니다. 처음에 "적절한 ReLU" 로 시작할 수 있다고 해도 만약 update를 지나치게 크게 해 버려 가중치가 날뛴다면 Dead relu영역에 들어갈 수 있습니다. 그래서 처음에는 학습이 잘 되다가 갑자기 죽어버리는 경우가 생기는 것입니다. 실제로 잘된 학습이여도 10~20%는 dead relu가 발생하며 학습에 지장은 없습니다.

6-28 그래서 사람들은 초기화시 0.01을 더해주기도 하는데 별 효과는 없습니다.

6-29 다음은 Leaky ReLU입니다. Leaky ReLU는 음수 역역에 기울기를 추가해 saturate되는 부분이 없으며 max함수를 사용해 효율적입니다. 포인트는 Dead relu가 없어졌다는 것입니다.

6-30 기울기가 알파 파라미터로 결정되는데 임의로 정하는 것이 아닌 backpro로 학습시키는 파라미터로 결정됩니다.

6-31 Leaky lelu와 비교하면 elu는 nagative부분에서 기울기를 가지는 동시에 saturation 됩니다. Elu에 주장에 따르면 이러한 saturation이 노이즈에 더강인하다고 합니다. Elu는 relu와 leaky relu의 중간이라고 보시면됩니다.  Zero-mean에 가까운 출력이지만 saturation된다는 점에서 relu와 비슷합니다.

6-32입력을 받아들이는 기본 형식을 가지고 있지 않습니다. 기본 내적은 선형을 따르지만 max함수를 통해 비선형을 보이고 있습니다!. 단점은 두개의 선형결합으로 파라미터와 뉴런의 수가 두배라 계산량이 많아집니다.

결론 1. 가장 먼저 ReLU사용하자, Leaky ReLU/Maxout/ELU도 시도해보면 좋습니다. sigmoid는 절대 사용하지말자!

이전다음

0123456

6-34 이번엔 데이터 전처리에 대해 알아보겠습니다.

6-35 데이터 전처리에는 zero-centered와 nomailzed가 있습니다. 왜 사용할까요?

6-36 앞서 sigmoid의 예에서 모든 입력변수가 양수일 경우에 대해 단점을 이야기했습니다. 기본적으로 image데이터는 pixel값을 가지고 있으므로 모두 양수입니다. 그러므로 입력차원에서 전처리를 통해 모든 입력이 양수가 되는걸 방지하자는 의미로 사용하게됩니다.

6-37 znormalization을 해주는 이유는 모든 차원이 동일한 범위안 있게 해줘서 전부 동등한 기여(contribute)를 하게 합니다. 기본적으로 이미지의 경우 각 차원간의 스케일이 맞춰져 있어 사용하지 않고 zero-centered만 해줍니다.

6-38 그리고 Machine learning 에서는 PCA나 whitening 같은 더 복잡한 전처리 과정도 있긴 합니다만 이미지에서는 단순히 zero-mean 정도만 사용하고 normalization 그 밖의 여러 복잡한 방법들은  잘 안씁니다.

6-39 요약해보자면 이미지 전처리에서는 대부분 zero-mean으로 해줍니다. 일부 모델들은 채널 전체를 계산해서 빼주는 경우도 있지만 각 채널을 독립적으로 생각해서 빼주는 경우도 있습니다. 이는 판단하기 나름입니다.

6-40 또 ResNet의 경우 각 채널의 표준편차를 나누어주기도 합니다.

이전다음

012345678910111213

6-40 이제 weight를 어떻게 초기화시켜야 하는지를 알아보겠습니다.

6-41 초기값을 0으로 설정하면 어떨까요 답부터 이야기하면 매우 나쁜 아이디어 입니다. 모두 0으로 해서는 안되는 이유는 뭘까요? 바로 backpropagation에서 모든 가중치의 값이 똑같이 갱신되기 때문입니다. 예를 들어 2층 신경망에서 첫 번째와 두 번째 층의 가중치가 0이라고 가정하면 순전파 때는 입력층의 가중치가 0이기 때문에 모두 같은 값이 전달될 것이고 같은 값이 입력된다는 것은 두번 째 층의 가중치가 똑같이 갱신된다는 의미입니다. 이는 가중치가 가지는 의미가 사라집니다.

6-41 이해가 안간다면 조금 쉬운 예를 들어보겠습니다. 헬기를 타고 산에 어느 지점에 떨어졌습니다. 안개가 자욱하여 앞이 안보이는 상황에서 밑으로 내려가야합니다. 어떻게 내려갈까요? 발의 느낌을 통해 경사를 보고 내려갈 것입니다. 초기화값을 0으로 설정한다는 것은 헬기가 같은 장소에 떨어 뜨린다는 걸 의미합니다. 그렇다면 앞이 안보이며, 같은 지점이라고 생각하지 못하기 때문에 몇번을 시도해도 같은방향으로 내려갑니다. 이러한 이유로 초기값을 0으로 설정하면 안된다는 겁니다.

6-42 처음의 아이디어는 0대신에 작은 random값을 가지는 숫자를 넣어보자 입니다. 표준편차가 0.01이며 가우시안 분포를 가지는 숫자를 넣어봅니다.

6-43 이러한 아이디어는 작은 네트워크에는 잘 작동하나 네트워크가 깊어질수록 문제가 생깁니다.

6-44 10개의 레이어가 500개의 뉴런을 가지는 네트워크를 한번 보겠습니다. 활성함수로 tanh인 비선형함수를 사용하였고, 초기값을 6-43슬라이드의 값을 사용했습니다.

6-45 왼쪽 그림의 평균은 2번째 step부터 0에 가깝게 형성되었는데 tanh함수 자체가 zero-mean이기 때문에 당연합니다. 문제는 표준편차입니다. 오른쪽 그림의 표준편차 또한 가파르게 0에 가까워지고 있습니다. 

6-46 첫 번째 레이어는 가우시안과 비슷한 좋은 분포를 형성하고 있습니다. 하지만 문제는 w를 곱할 수록 w가 너무 작은 값이라서 출력값이 줄어들게 됩니다. 결국 0이 됩니다. 자그럼 이상황에서 packprop를 생각해봅시다 x가 엄청 작은 값이기 때문에 gradint도 작을것이고 업데이트가 잘 일어나지 않을 것 입니다. Backprop 를 생각해보면 내려가면서 local gradient가 곱해지는데 local gradient는 입력X입니다. X가 엄청 작은 값이기 때문에 gradient는 작을 것이고 결국 업데이트는 일어나지 않습니다.

6-47 그럼 가중치의 편차를 크게 하면 어떻게 될까요 여기서는 0.01대신 1을 사용해보겠습니다.  가중치가 큰값을 가지니까 tanh의 출력은 항상 -1또는 1로 saturation될 것입니다.

6-48 가중치를 어떻게 주면 훈련을 잘할 수 있을까 고민중에 나온것이 Xavier initialization입니다. 앞서 표준편차가 1 또는 0.01인 정규분포와 달리 Xavier initialization은 앞 계층의 노드가 n개라면 표준편차가 1/루트n의 분포를 사용합니다. Xavier initialization이 하는 일은 입 출력의 분산을 맞춰주는 것입니다. 입력의 수가 작으면 작은값으로 나누고 크면 큰값을 나눕니다. 쉽게말하면 탄젠트로 들어오는 값이 x와 w의 내적의 합인데 이게 인풋이 많아지면 합이 커지면서  saturation됩니다 그래서 saturation을 막기위해 w의 갑을 인풋에 맞게끔 줄여줍니다.

6-49 문제점이 하나 있는데 ReLU를 사용하면 잘 작동하지 않습니다. 이유는 렐루는 출력의 절반을 죽여버립니다. 절반은 0이 됩니다. 그렇다면 출력의 분산을 반토막냅니다. 여기 그림을 보면 처음 layer부터 많은 부분이 0이 되고 점점 많은 값이 0이됩니다.

6-50 이러한 문제점을 해결하기 위해 나온 것이 He initialization입니다.ReLU는 출력의 절반을 죽이기 때문에 Xavier에서 2만큼 한번더 나누어 줍니다 보면 잘 작동하는걸 볼 수 있습니다. 실제 ReLU 입력은 반밖에 안들어가므로 반으로 나눠줍니다.

6-51 그래프를 보면 잘 작동하는 걸 볼 수 있습니다.

이전다음

012345678

6-53 가중치의 초깃값을 적절히 설정하면 각 층의 활성화 값 분포가 적당히 퍼지면서 학습이 원활하게 수행됨을 배웠습니다. 그렇다면 강제로 적당히 퍼트리도록 하면 어떻게 될까요? 배치 정규화가 그런 아이디어에서 출발한 방법입니다.

Batch Normalization의 장점은 1. 학습을 빨리할 수 있습니다. 2. 초깃값에 크게 의존하지 않습니다.(매우 환영) 3. 오버피팅을 억제해줍니다.

6-54 또한 미분 가능한 함수입니다. 평균과 분산을 "상수" 로 가지고만 있으면 언제든지 미분이 가능하며 따라서 

Backprop이 가능하게 됩니다.

6-55 배치당 N개의 데이터와 D차원이있는데 차원당 평균과 분산을 구해주고 정규화 해줍니다. 이건 fc일 경우이며,

CNN경우 activation map당 평균과 분산을 계산해줍니다.

6-56 BN의 경우 활성화 함수 전에 FC나 CNN layer후에 넣어줍니다.

6-57 그러나 한가지 의문이 있습니다. FC layer를 거칠 때 마다 매번 normalization를 해주는 것에 대한 의문이 있습니다.

우리가 정말 tanh의 입력이 unit gaussian이기를 바라는 것일까요? normalization이 하는 일은 입력이 tanh의 linear한 영역에만 존재하도록 강제하는 것입니다. 그렇게 되면 saturation이 전혀 일어나지 않게 됩니다. saturation이 아예 일어나지 않는 것 보다 조절할 수 있으면 좋겠죠? 이 부분은 6-31에서 Elu를 알아보며 saturation이 노이즈에 강인하다는 점을 배웠습니다.

6-58 Batch normalization에서는 normalization연산(왼쪽 상단)이 있었습니다. 감마와 베타가 추가되었습니다. 감마로는 스케일링 베타로는 이동의 효과를 줍니다. 네트워크를 원상복구 하고 싶다면 감마를 = 분산 베타를 = 평균으로 하면 됩니다. 이렇게 감마와 베타를 적용하면 얼마나 saturation 시킬지를 학습하기 때문에 유연성을 얻을 수 있습니다. 또 앞에서 노이즈에 강하다는 이야기가 있었는데 그거와도 일맥상통한다고 생각합니다.

6-59  Batch normalization를 다시한번 요약해 보자면 입력이 있고 mini-batch를 통해 평균을 계산합니다. 그리고 분산도 계산합니다. 평균과 분산으로 normalize 한 이후에 감마와 베타를 통해 scaling과 shifting을 사용합니다. BN은 gradient의 흐름을 보다 원활하게 해주며 결국 더 학습이 더 잘되게(robust) 해줍니다. BN을 쓰면 learning rates를 더 키울 수도 있고 다양한 초기화 기법들도 사용해 볼 수 있습니다. 또하나 regularization의 역할도 한다는 것입니다. 각 레이어의 출력이 하나의 데이터의 영향을 받은 것이 아닌 batch안에 모든 데이터의 영향을 받아  regularization 효과를 줍니다.

6-59 그래프는 초기값에 따른 epoch마다 accuracy를 나타낸 그래프입니다. BN을 사용할 경우 초기값에 영향을 받지 않는 것을 그래프를 통해 볼 수 있습니다.

이전다음

012345678910111213

6-61 이제 학습과정을 다루는법에 대해 알아보겠습니다. 지금까지 네트워크 설계를 배웠습니다. 이제는 학습과정을 어떻게 모니터링하고 하이퍼파라미터를 조절할 것인지를 배워보겠습니다.

6-62 첫 단계는 데이터 전처리 입니다. 앞에서 배운 것 처럼 zero-centered를 해줍니다.

6-63 50개의 뉴런을 가진 하나의 hidden layer를 학습해보겠습니다.

6-64 Forward pass를 하고난 후에 Loss가 그럴듯해야 합니다. Softmax classifer의 로스는 negative log likelihood가 되어야합니다. 10개의 클래스라면 Loss는 -log(1/10) = 2.3 이니 잘 작동합니다.

6-65 지금까지는 여기 regularization을 0으로 설정하였습니다. 앞서 계산한 2.3은 regularization을 사용하지 않은 상태입니다. 여기에 regularization을 추가하면 Loss가 증가합니다. regularization이 더해지니 Forward pass시 로스가 증가하는 것은 당연하겠죠?

6-66 처음 시작할 때는 데이터의 일부만 학습하는게 좋습니다. 데이터가 적으면 오버핏이 생기고 로스가 많이 줄어듭니다. 이때는 regulaization을 사용하지 않고 단지 로스가 내려가는지 확인합니다. CIFAR-10데이터에서 20개의 샘플을 사용하며 10개의 클래스를 가집니다. optimizer는 SGD를 사용합니다.

6-67 loss는 줄어들고 accuracy는 100%를 달성합니다. overfit 되었습니다.

6-68 Sanity chack가 끝나면 본격적으로 훈련할 차례입니다.이제는 전체 데이터 셋을 사용하고 regularization을 약간씩 주면서 적절한 learning rate를 찾아야합니다. learning rate은 가장 중요하고가장 먼저 정해야만합니다.

6-69 loss가 거의 변화하지 않습니다.

6-70 그 이유는 learning rate이 매우 작기 때문입니다.

6-71 그렇다면 loss의 변화는 없지만 정확도는 올라갔을까요? 그 이유는 손실함수는 조금 씩 옳은 방향으로 갑니다. 정확도는 그저 가장 큰값만 취하기 때문에 크게 오를 수 있습니다.

6-72 learning rate을 1e6으로 학습해보겠습니다.

6-73 loss가 발산하는 것을 볼 수 있습니다. learning rate이 너무 작으면 loss의 변화가 없고 너무 크면 발산해버립니다.

6-74 3e-3또한 너무 높아 발산합니다. 보통 learning rate은 1e-3 ~ 1e-5범위를 사용해서 cross valiation을 통해 결정합니다.

이전다음

01234567891011121314

6-75 이제 하이퍼파라미터 최적화에 대해 알아보겠습니다. 어떻게 최적화 할까요? 앞서 말씀드렸습니다. cross valiation을 통해 최적화시킬 수 있습니다.

6-76 cross valiation은 train set을 다시한번 train과 val로 분류한 후 Coarse stage에서 넓은 범위에서 값을 골라냅니다.

Epoch 몇번 만으로도 잘 동작하는지 알 수 있습니다. 예를 들어 NaN이 뜨거나 loss가 줄지 않거나 Coares stage가 끝나면 어느 지점에서 잘 작동한다 알 수 있고 좀 더 좁은 범위를 설정하고 학습을 길게 시켜 최적의 값을 찾습니다. NaN로 발산하는 징조를 미리 감지할 수도 있습니다. 이전의 cost보다 3배 높아졌다면 잘못 하고 있는 것입니다. 이런 경우 다른 하이퍼파라미터를 선택합니다.

6-77 예로 5epochs를 통해 Coares stage를 해보겠습니다. 여기서 볼것은 acc가 높은 곳을 빨간색으로 표시했는데 이부분을 중심으로 fine stage를 할 것입니다. 

6-78 Coares stage를 통해 얻는 범위로 다시 학습합니다.

6-70 가장 높은 val_acc를 얻은 부분이 있습니다. 그렇다면 이때의 learning rate이 Best일까요? 잘 보면 좋은 learning rates은 전부 1e-4 사이에 존재하고 있습니다. Coares stage에서 얻은 결과를 통해 설정한 범위에 집중되어있습니다. 이것은 좋지 않습니다. learning rate을 효율적으로 탐색할 수 없기 때문입니다. 1e-5에서 최적의 learning rate이 있을 수 있습니다. 보통 최적의값을 범위의 중앙에위 치합니다.예를들어 1e-4일 경우 1e-3~1e-5의 범위로 찾습니다.

6-80 하이퍼파라미터를 최적화시키는 방법에는 Random Search와 Grid Search가 있는데, Random Search가 좋습니다. Grid Search의 경우 그림과 같이 3번의 샘플링밖에 하지못해 좋은 하이퍼파라미터를 찾기에 제한이있습니다.

6-81 하이퍼파라미터는 턴테이블을 만지는 것과 같다...

6-82 cross valiation을 진짜 많이해봐야 한다..

6-83 learning rate이 적절한지는 epoch당 loss의 그래프를 보면 직관적으로 알 수 있습니다. learning rate이 높을 경우 loss는 발산하며 매우 낮을 경우 천천히 수렴합니다.

6-84 가끔 이런 그래프를 볼 수 있는데

6-85 이런경우 초기값의 설정이 잘못된 것입니다.

6-86 train과 val사이의 gap이 크다면 regularization을 고려해볼 수 있으며 gap이 작다면 모델의 성능이 올라갈 가능성이 있습니다.

6-88 요약하자면 활성화함수로는 ReLU를 사용하며 전처리의 경우 zero-centered가 되게 하며 Xavier초기값을 많이 사용합니다. Batch Normalization을 사용합니다. 이런점은 현재 2019년에도 비슷하게 적용됩니다.